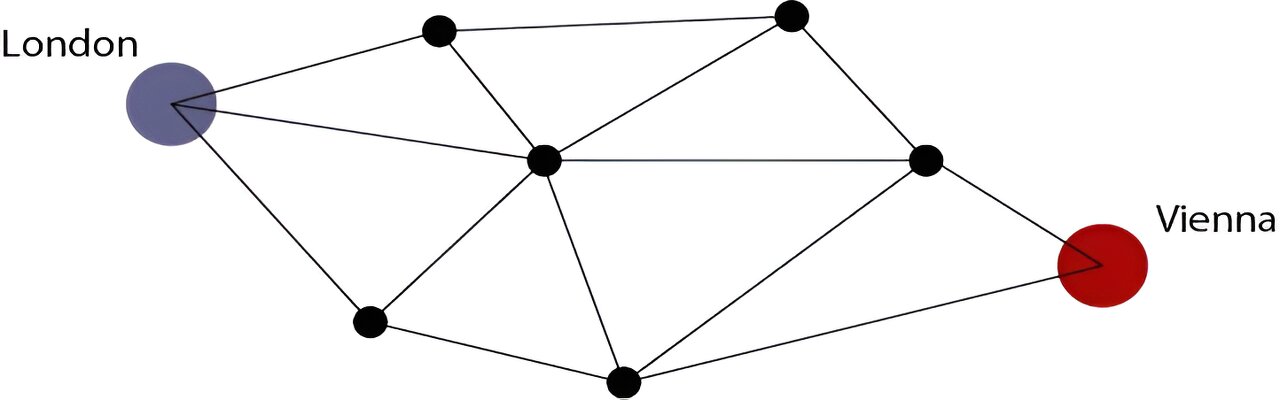
New Algorithm Accelerates Shortest Path Discovery
Researchers have developed a new algorithm that breaks the long-standing sorting barrier in shortest-path problems, enabling faster computation on both directed and undirected graphs without relying on sorting, potentially revolutionizing network analysis and routing algorithms.