mathematics9.84 min read
The 9th Dedekind Number: A 32-Year Quest and the Elusive 10th
19 days ago•Source: IFLScience
Mathematics News
The latest mathematics stories, summarized by AI
Featured Mathematics Stories
View original source
8.205 min•25 days ago
Highlights of the Year in Mathematics
The article highlights the artistic and exploratory nature of mathematics through stories of young prodigies like Hannah Cairo, breakthroughs in understanding infinity and quantum fractals, the legacy of Maryam Mirzakhani, and recent discoveries such as the Noperthedron and new types of infinity, illustrating the ongoing quest to understand the fundamental structures of math and the universe.
More Top Stories
2
New Method Unravels Knot Measurement Simplicity
Quanta Magazine•3 months ago
3
Student Resolves Long-Standing Addition Limit Issue
WIRED•6 months ago
More Mathematics Stories
"Predicting Prime Numbers: A Groundbreaking Breakthrough"
Originally Published 1 year ago — by Phys.org
Researchers at City University of Hong Kong and North Carolina State University have made a groundbreaking discovery in prime number theory, challenging the long-held belief that prime numbers are unpredictable. Their research has led to the development of a Periodic Table of Primes (PTP) that can accurately predict the locations of prime numbers, with potential applications in fields such as cybersecurity. This breakthrough has the potential to significantly impact encryption and cryptography, making data more secure.
"Michel Talagrand Awarded 2024 Abel Prize for Taming Randomness"
Originally Published 1 year ago — by Quanta Magazine
French mathematician Michel Talagrand has been awarded the Abel Prize for his groundbreaking work in probability theory and understanding random processes. His research has revolutionized the field, providing insights into the behavior of complex systems and developing techniques to analyze extreme outcomes and concentration phenomena. Talagrand's work has had a profound impact across various disciplines, from mathematics and physics to computer science and statistics, and he has dedicated himself to sharing his knowledge through textbooks and mentoring young researchers.
"Mathematicians Solve 70-Year-Old Music Geometry Puzzle"
Originally Published 1 year ago — by SciTechDaily
Researchers have made a breakthrough in spectral geometry by proving a special case of Pólya’s conjecture related to the eigenvalues of a disk, a problem in mathematics first formulated in 1954. This work not only highlights the universal value and artistic beauty of mathematical research but also has potential practical applications in computational mathematics and numerical computation. The researchers' achievement, published in the mathematical journal Inventiones Mathematicae, represents a significant advance in understanding the geometry of music and wave propagation.
"Mathematicians Solve 70-Year-Old Disk Eigenvalues Conjecture"
Originally Published 1 year ago — by Phys.org
Mathematicians, including Iosif Polterovich and his collaborators, have proven a special case of George Pólya's 70-year-old conjecture in spectral geometry, concerning the estimation of the frequencies of a round drum or the eigenvalues of a disk. This achievement, published in Inventiones Mathematicae, has theoretical value and potential applications in computational mathematics and numerical computation. The researchers' success highlights the universality of mathematics and the pursuit of elegant solutions with practical implications.
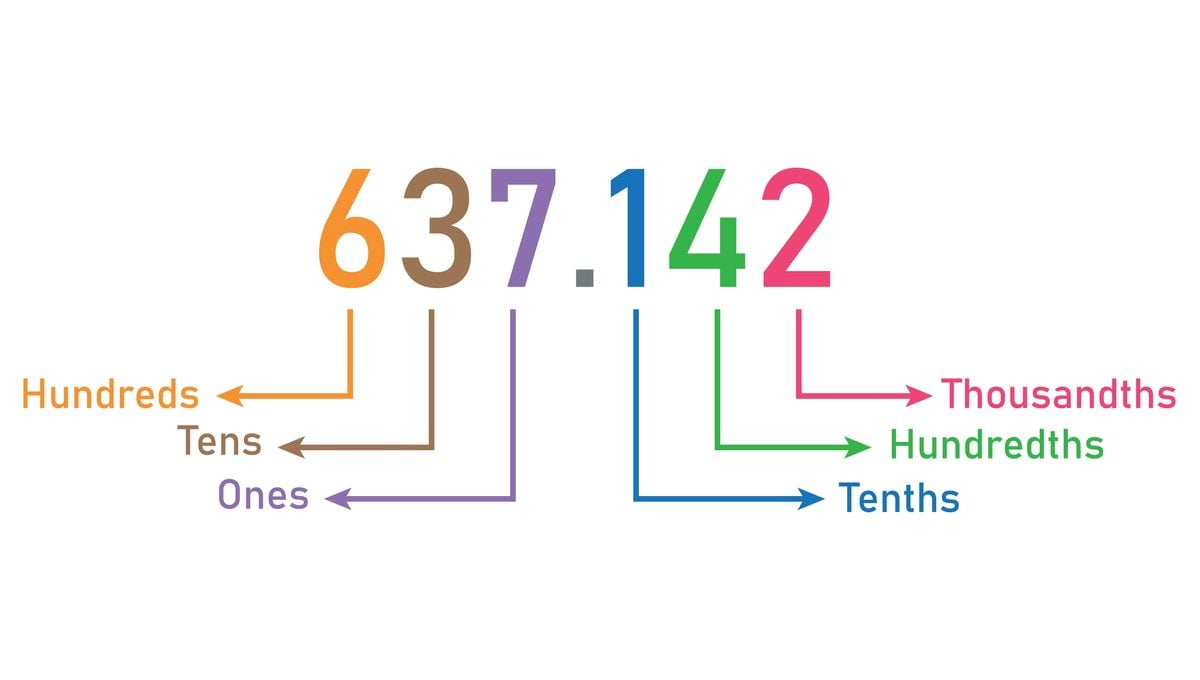
"Discovery: Decimal Point Found in 1440s Italian Merchant's Notes"
Originally Published 1 year ago — by IFLScience
The use of the decimal point in mathematics dates back further than previously thought, with a new paper tracing it back to the work of Giovanni Bianchini in the 1440s. Bianchini, a Venetian merchant and administrator, used the decimal system in his calculations in spherical astronomy and metrology, introducing the notation of a little dot to separate whole units from the fractional part. This notation was later adopted by influential mathematician astronomers such as Clavius and Regiomontanus, shaping the development of mathematical notation and paving the way for the widespread use of the decimal point.
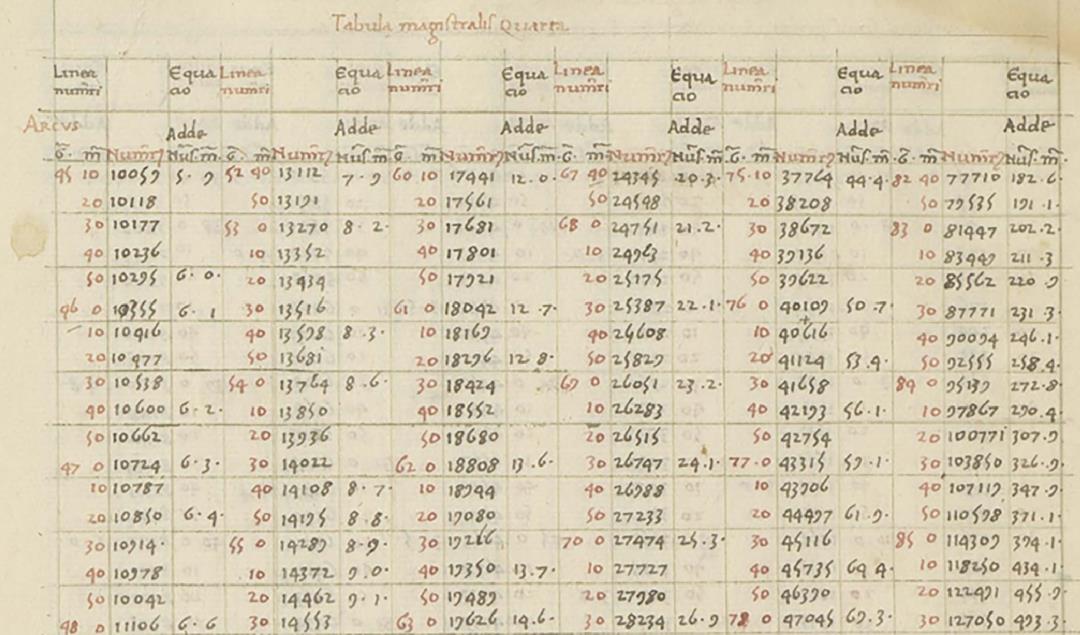
"Discovery: Decimal Point Found in 1440s Merchant's Notes"
Originally Published 1 year ago — by Newser
Math historian Glen Van Brummelen discovered a decimal used to indicate tenths of a number in a 15th-century treatise, challenging the belief that German mathematician Christopher Clavius was the first to use decimals in a 1593 treatise. The treatise by Venetian merchant Giovanni Bianchini, using a base-10 system, marked a significant advancement in calculations, potentially influencing Clavius's work. This finding sheds new light on the history of decimals and their early usage in mathematical calculations.
"Revised History: Decimal Point Usage Found to be 1.5 Centuries Older Than Previously Believed"
Originally Published 1 year ago — by Phys.org
Glen Van Brummelen, a mathematical historian, has discovered evidence of a decimal point being used by a Venetian merchant, Giovanni Bianchini, in the 1440s, 150 years before its previously known use by Christopher Clavius. This finding suggests that the use of the decimal point to represent non-whole numbers occurred much earlier than previously thought, potentially influencing the development of math fundamentals. Bianchini's background as a merchant and his travels to places in the Islamic world may have influenced his use of non-whole numbers and ways to represent them more easily.
"Establishing a Statistical Mechanics Backbone with Maze Proof"
Originally Published 1 year ago — by Quanta Magazine
Mathematicians have long been intrigued by randomly generated mazes on hexagonal grids and the critical probability at which the character of the maze changes drastically. A recent paper has calculated the chance of finding a path for mazes at the critical probability of 1/2, shedding light on the behavior of these mazes. The study has practical applications in various fields, from designing gas masks to understanding the spread of infectious diseases. The research also delves into the computation of elusive exponents, such as the monochromatic two-arm exponent, and explores the mathematical properties of SLE curves within the maze.
Unraveling the Essence of "Good" Mathematics
Originally Published 1 year ago — by Quanta Magazine
Mathematician Terence Tao revisits the question of what constitutes "good" mathematics in a podcast with Steven Strogatz, reflecting on the diverse values and approaches within the field. Tao emphasizes the convergence of different ideals toward a common objective of "good mathematics," highlighting the importance of grounding mathematical research and the interconnections between different areas of mathematics. He also discusses the philosophical belief that mathematics represents an objective reality waiting to be discovered, and the importance of embracing diverse insights and perspectives in the pursuit of mathematical knowledge.
Unraveling the Mysteries of the Mandelbrot Set
Originally Published 1 year ago — by Quanta Magazine
The Mandelbrot set, a famous fractal shape, captivated mathematicians and the public in the 1980s but later faded into obscurity. However, a group of mathematicians has continued to unravel its mysteries, with recent progress made towards proving the long-standing MLC conjecture. The Mandelbrot set's intricate geometry has led to the development of sophisticated techniques that have transformed the study of dynamical systems. The set's founders, Pierre Fatou and Gaston Julia, pioneered the study of iterated functions, which later inspired Benoît Mandelbrot to use computer graphics to bring complex dynamics to the forefront. The MLC conjecture, which posits that the Mandelbrot set is locally connected, has become one of the field's deepest and most important open conjectures.