tldrdaily.news logo
Tag

Aperiodic Monotile

All articles tagged with #aperiodic monotile

science2 years ago

Mathematicians finally discover the elusive 'Spectre' aperiodic tile.

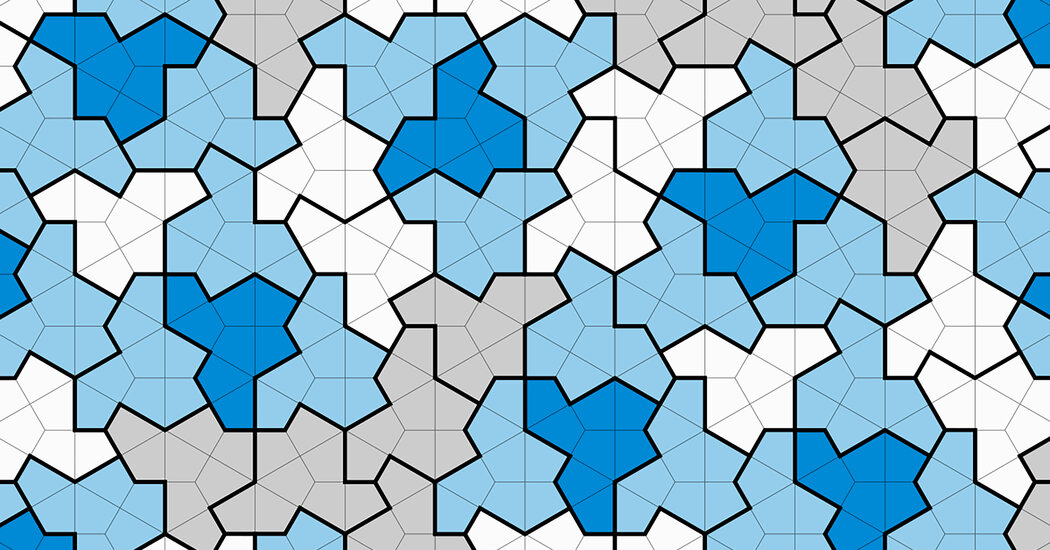
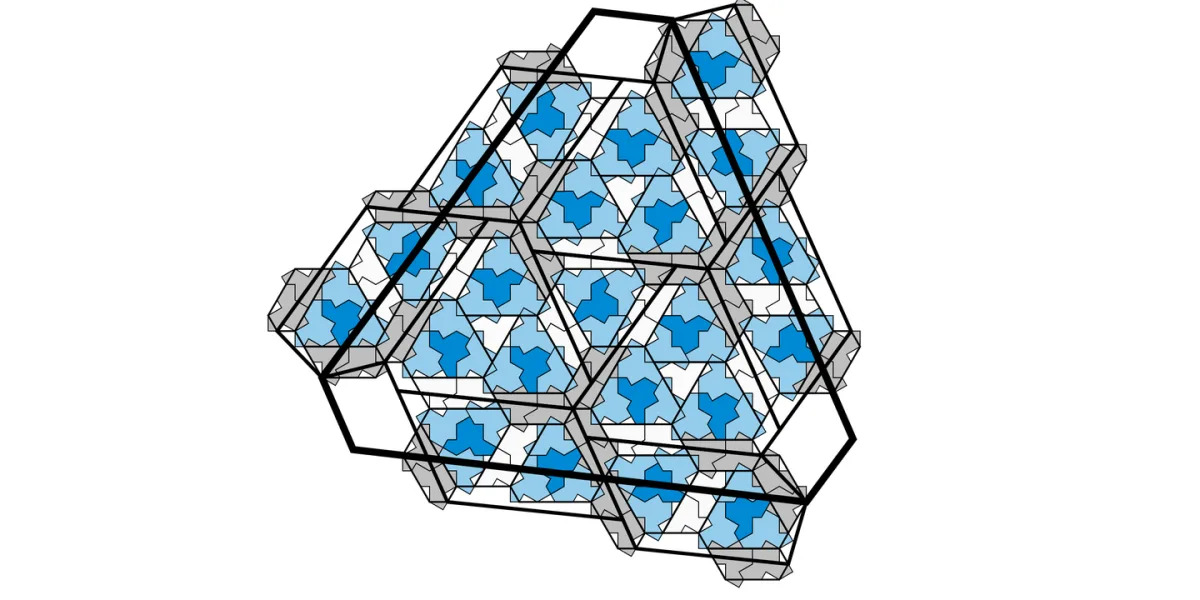
Mathematicians have discovered a 14-sided shape called the "Spectre" that can tile a surface without ever repeating or being flipped. The shape is the first example of an aperiodic monotile that tiles the plane without reflections. The discovery is the culmination of decades of hunting by mathematicians around the world, and it was made by a retired printing technician named David Smith. The team started with the original "hat" shape and added an extra side to it. That new shape still required its mirror image to fully tile, but the researchers discovered that by transforming the 14-sided shape's straight edges into curved ones, they could dispense with mirror images and work with just the one shape.

via Livescience.com|
#aperiodic-monotile#david-smith#mathematics
science2 years ago

'Mathematicians discover elusive 'vampire Einstein' shape'

Mathematicians have discovered a 14-sided shape called "Spectre" that can tile a surface without repeating or being flipped, making it the first example of an aperiodic monotile that tiles the plane without reflections. The shape was discovered by adding an extra side to the original "hat" shape and transforming its straight edges into curved ones. The discovery culminates decades of hunting by mathematicians around the world for a shape that could completely tile a surface without ever repeating.

via Yahoo Life|
#aperiodic-monotile#mathematics#science
science-and-technology2 years ago

Mathematicians Crack Decades-Long Tiling Puzzle with Upgraded Einstein Shape

Researchers have discovered a new-and-improved "einstein" - a single shape that tiles a plane, or an infinite two-dimensional flat surface, but only in a nonrepeating pattern. The new monotile discovery does not use reflections and is a close relative of the original "hat" einstein. The team produced a family of strong or "strictly chiral aperiodic monotiles" through a simple modification of the T(1,1) tile, named "Spectres," which only allow nonperiodic tilings, and without reflections.

via The New York Times|
#aperiodic-monotile#einstein#mathematics
mathematics2 years ago

New Shape Discovered Solves Longstanding Math Problem

After a decade of attempts, David Smith, a shape hobbyist, has discovered an "einstein," an aperiodic monotile that tiles a plane in a nonrepeating pattern. Smith's einstein, called "the hat," is a polykite made of eight kites. The paper, co-authored by Smith and three others, provides two proofs of the hat's aperiodicity, one of which uses a new technique. The hat's discovery opens up new possibilities for materials with this type of internal structure.

via Yahoo! Voices|
#aperiodic-monotile#einstein-problem#mathematical-proof
digital-art2 years ago

Mathematicians Discover Mesmerizing Non-Repeating Shape with Unique Properties

Mathematicians have discovered a new 13-sided two-dimensional shape called the 'Hat', which can be used indefinitely in a pattern without ever repeating. The Hat is an aperiodic monotile, meaning a single tile can be used across an entire surface without ever repeating. The discovery of this new shape could open up new design and graphic design challenges and ideas, providing designers and artists with a new shape to play with. The Hat's angles and 13-sides could make it a tricky one to work into new logos and projects, but it could be used in tiled floors, fabric patterns, and designer wallpaper.

via Creative Bloq|
#aperiodic-monotile#design#digital-art
mathematics2 years ago

Mathematical mystery solved by elusive 'Einstein'.

After a decade of attempts, a self-described shape hobbyist from England, David Smith, has discovered an "einstein," an aperiodic monotile that tiles a plane in a nonrepeating pattern. Smith's discovery, called "the hat," was confirmed in a new paper by Smith and three co-authors with mathematical and computational expertise. The paper provides two proofs, one of which offers a new tool for proving aperiodicity. The hat is a polykite made of eight kites and is part of an entire family of related einsteins, including a second one discovered by Smith called "the turtle."

via The New York Times|
#aperiodic-monotile#einstein-problem#mathematical-proof
science2 years ago

"New 13-Sided Shape Defies Repetition and Unleashes Remarkable Potential"

Computer scientists have discovered a new shape called the "einstein," which has 13 sides and can cover a plane without ever repeating. This shape is the first true aperiodic monotile, meaning it can tile a plane but never repeat. The discovery has applications in material science. The team proved the nature of the shape through computer coding, and it doesn't lose its aperiodic nature even when the length of sides changes.

via Yahoo Life|
#aperiodic-monotile#computer-science#material-science