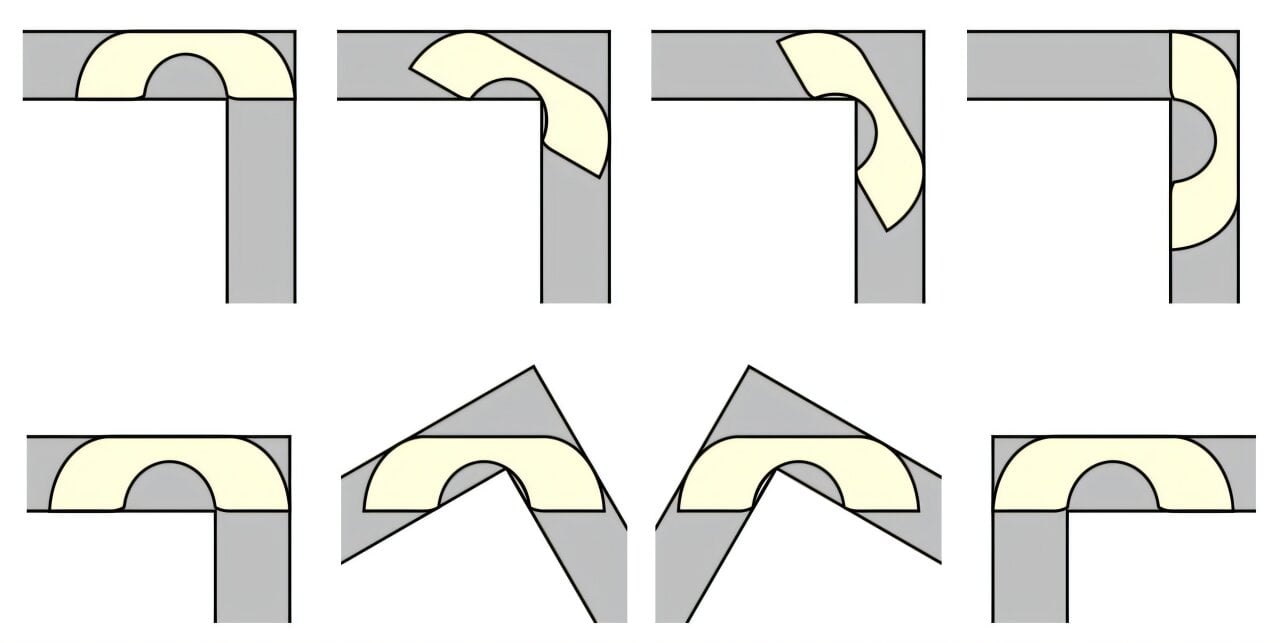
Mathematician Cracks the Moving Sofa Conundrum
Jineon Baek, a mathematician from Yonsei University, claims to have solved the moving sofa problem, a mathematical challenge posed by Leo Moser in 1966. Baek's proof, posted on arXiv, uses the Gerver sofa shape to determine that the maximum area of a sofa that can navigate a right-angled hallway of one unit width is 2.2195 units. The proof awaits validation by the mathematical community.