"Confirming the Low-Rank Hypothesis in Complex Systems"
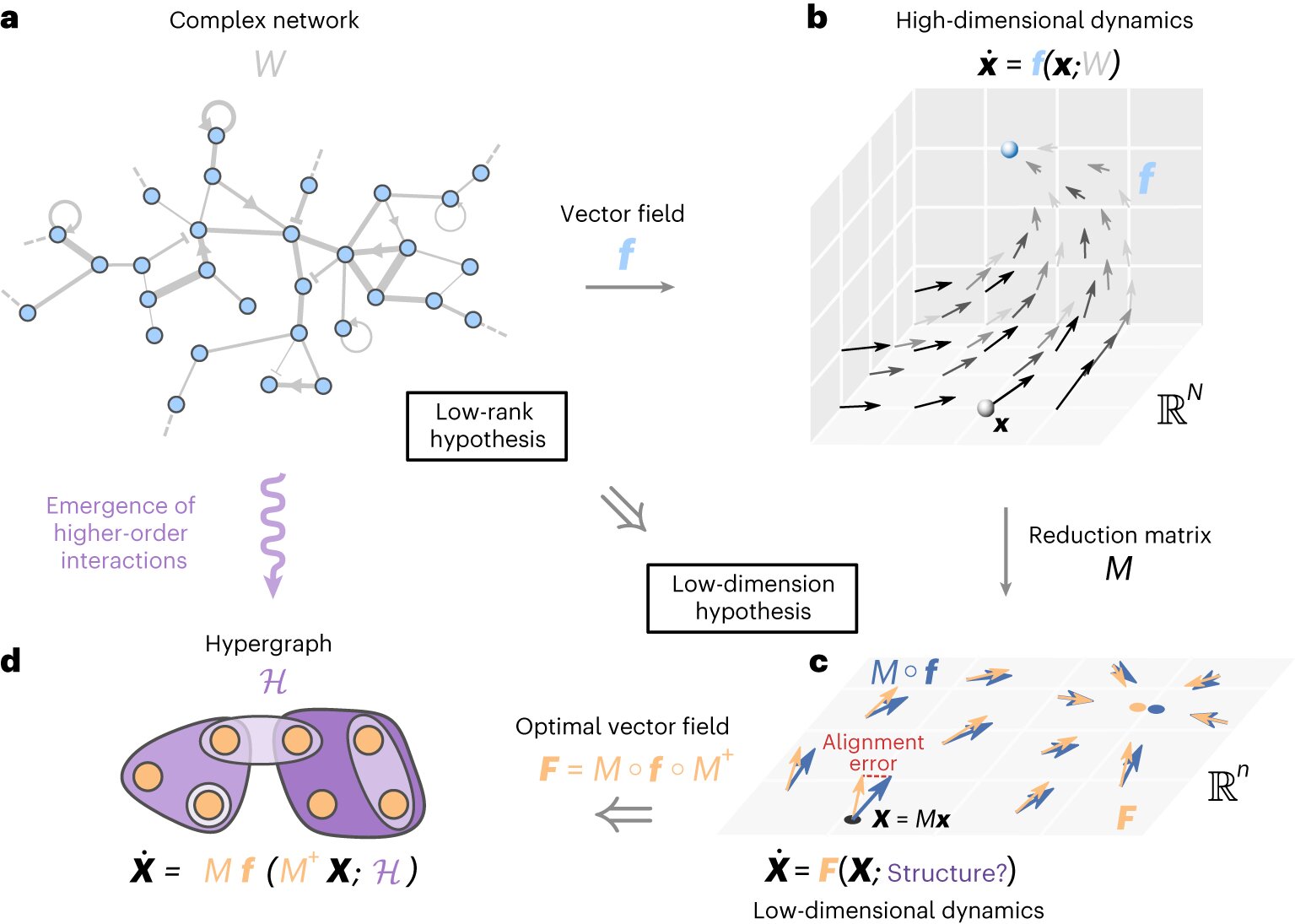
Scientists have investigated the low-rank hypothesis in complex systems, finding that despite high-dimensional nonlinear dynamics, many real networks exhibit rapidly decreasing singular values, supporting the feasibility of effective dimension reduction for understanding and modeling complex system behaviors. The study, published in Nature Physics, aims to address the challenge of understanding large-scale behavior in complex systems by exploring the intrinsic simplicity of these systems and finding an optimal dimension for simplifying models. The researchers sought to validate the low-rank hypothesis using singular value decomposition, a powerful mathematical tool from linear algebra.




